Picture


ACADEMIC BACKGROUND:
​
​My name is Christoph Jansen. I'm a postdoctoral researcher and habilitation candidate at the Department of Statistics of LMU Munich. During summer semster 2022 I was interim professor for Statistics. I obtained a Ph.D. in Statistics with a thesis on decision making in complex information settings at the same Department in July 2018 under the supervision of Thomas Augustin. After that, I worked as a math teacher at a business school for about two years. Since April 2021 I'm back in academia.

On this site, I collect information about my research and teaching activities. This includes links to published papers, links to preprints or work in progress, presentation slides of recent conference talks, and lecture notes.


​
​MOST RECENT PUBLICATIONS: 

  • Christoph Jansen, Malte Nalenz, Georg Schollmeyer and Thomas Augustin (2023): Statistical comparisons of classifiers by generalized stochastic dominance. Journal of Machine Learning Research,  24: 1 - 37. [link]

  • Christoph Jansen, Georg Schollmeyer, Hannah Blocher, Julian Rodemann and Thomas Augustin (2023): Robust statistical comparison of random variables with locally varying scale of measurement. In: Proceedings of the Thirty-Ninth Conference on Uncertainty in Artificial Intelligence (UAI 2023). Proceedings of Machine Learning Research, vol. 216. PMLR. [link]



MAIN RESEARCH INTERESTS:

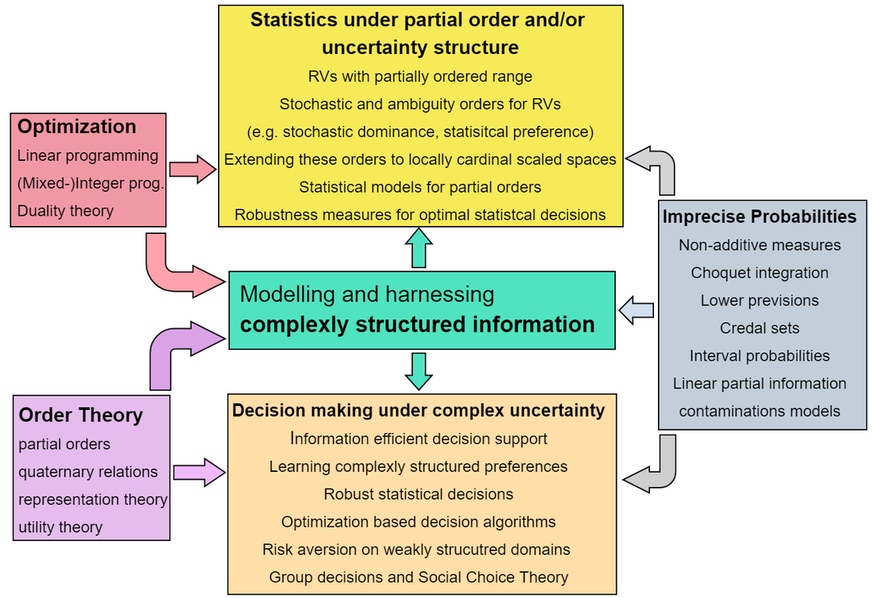
  • Decision Theoretic Foundations of Machine Learning: On a general level, I am very interested in pretty much everything (even loosely) related to decision making under uncertainty, ranging from axiomatic theories to applications in substance matter contexts. More specifically, I mainly focus on decision-making under weakly structured information, where the weak structure can originate from partially ordered preferences or imprecise probabilistic information or both. Much of my work focuses on developing models formalizing such situations as well as algorithms for efficient decision support. Here, the main focus is always on what can be derived from such generalized modeling for statistical decision theory and machine learning. This is not least due to the fact that decision theory can be understood as a formal superstructure of most common statistical methods.

  • Optimization Theory:  When applying decision theory to real-world problems, e.g. in the context of decision support algorithms and expert systems, optimization theory often plays a crucial role. I have a huge interest in developing new (linear) optimization-based algorithms for determining optimal decisions. Beyond that, I am also very interested in optimization theory  and approximation theory from a purely theoretical point of view.

  • Stochastic Orderings: Again mainly originating from a decision-theoretic point of view, I am also very fascinated by stochastic orderings.  When generalizing optimality criteria from classical decision theory to more complexly structured information settings, there often arise very nice and natural generalizations of classical stochastic orderings like e.g., (first-order) stochastic dominance or statistical preference. These generalizations then can be re-adapted to e.g. statistical contexts and applications, allowing for completely new perspectives also here.

  • Imprecise Probabilities: A significant part of my work is concerned with theories for describing and characterizing uncertainty beyond perfect stochasticity. Such theories, commonly summarized under the umbrella term imprecise probability theories, allow for very general models of uncertainty and, accordingly, for flexible and information-efficient descriptions of reality. Here, I am interested in both theoretical aspects (for instance non-additive measures, general integration theory) as well as the huge variety of applications in both Statistics and Decision Theory (for instance Robust Statistics or Choice Models accounting for Ambiguity).
​
​
Please feel free to check my papers and other stuff!

For a diagram summarizing my research interests, please see below.​

​LINKS: